Mean-Field Descriptions of Bursting Behavior in Networks of Spiking Neurons
Development and validation of mean-field models of spiking neural networks, studying phase transitions between asynchronous and synchronized bursting behavior.
This project is aimed at the development and validation of mean-field models of spiking neural networks. Such mean-field models represent direct mathematical descriptions of the macroscopic dynamics of a neural population and are beneficial for both the mathematical analysis of emergent behavior within a population and studies of larger networks of interconnected populations (see Fig. 1). Thus, mean-field models are an important tool for studying phase transitions in basal ganglia networks.
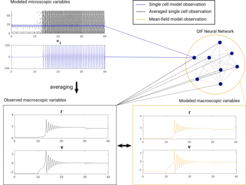
Figure 1: Relationship between variables of the mean-field model and spiking neural network. QIF = quadratic integrate-and-fire, r = firing rate, v = membrane potential.
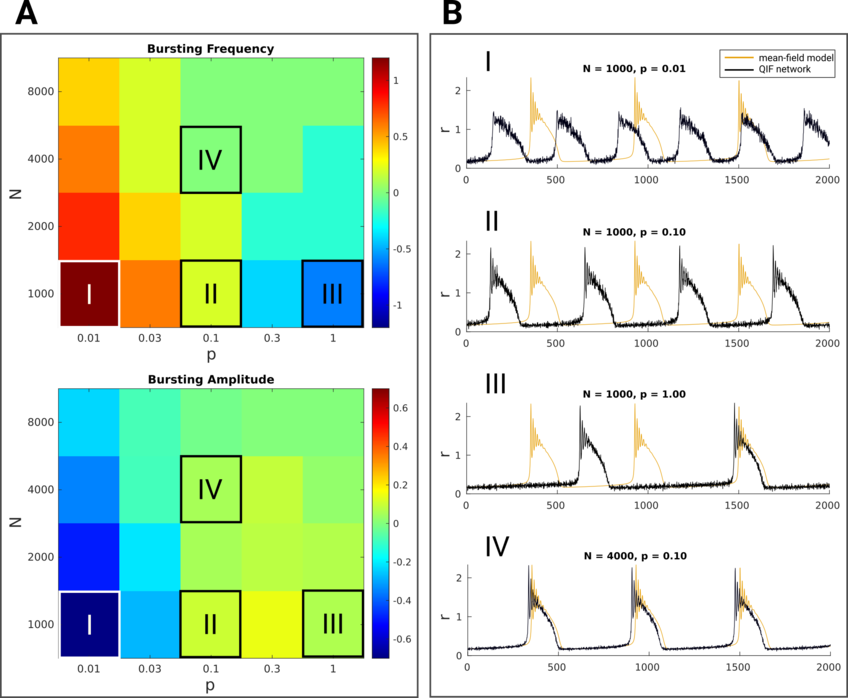
In a first step, we extended a mean-field model of globally coupled quadratic integrate-and-fire (QIF) neurons (see [1]) with different short-term adaptation mechanisms and examined their effects on the population dynamics via bifurcation analysis [2]. For the latter, we used the Python interface to the bifurcation software Auto-07p that comes with our self-developed dynamical systems software PyRates [3]. We found regimes of bursting behavior that emerged due to short-term adaptation in our model. Furthermore, we found a close correspondence between the mean-field model and spiking neural networks of different size and coupling density. In Fig. 2, we show the difference between the mean-field model and different spiking neural networks in terms of bursting frequency and amplitude.
Figure 2: Finite size analysis of bursting behavior. A: differences between the mean-field model and spiking neural networks with different size (N) and coupling probability (p) in terms of inter-burst frequency and peak intra-burst amplitude. B: Time series of mean-field model and spiking neural network bursting behavior for particular network sizes (N) and coupling probabilities (p).
[1] Montbrió E, Pazó D, Roxin A. Macroscopic Description for Networks of Spiking Neurons. Physical Review X. 2015; 5(2): 021028.
[2] Gast R, Helmut S, Knösche TR. A Mean-Field Description of Bursting Dynamics in Spiking Neural Networks with Short-Term Adaptation. bioRxiv. 2019; p. 806273. doi:10.1101/806273.
[3] Gast R, Rose D, Salomon C, Möller HE, Weiskopf N, Knösche TR. PyRates— A Python framework for rate-based neural simulations. PLOS ONE.2019; 14(12): e0225900. doi:10.1371/journal.pone.0225900.