Uncertainty and sensitivity analysis
Investigation of parameter uncertainties and sensitivities in computational models in the field of neuroscience.
In neuroscientific research, models play a central role. With their help we are able to relate different observable parameters, gain mechanistic insight into processes and systems, and make valid predictions. However, this strongly relies on the degree to which the model parameters are precisely known. Due to individual variability, measurement uncertainty, and other factors, this prerequisite is not strictly fulfilled. For this reason, in this project we are developing effective methods for investigating the influence of uncertain model parameters on the predictability of target variables. This involves two major concepts:
- Sensitivity describes the derivative of some output variable with respect to some parameter of the model. It of course depends on the chosen values for all model parameters (as long as the model is not linear).
- Uncertainty describes (the variance of) the probability distribution of the output variable given the probability distributions of all parameters. It can be split into portions associated to the separate parameters by computing the so-called Sobol coefficients. A Sobol coefficient related to a particular pair of output variable and model parameter can be small for two reasons: (1) the sensitivity of the output towards that parameter is small, and (2) the uncertainty (i.e., variance) of the parameter is small.
In order to quantify sensitivity and uncertainty in an efficient way, we have developed a technique based on the principle of non-intrusive generalized polynomial chaos (gPC). This method describes the relationship between model parameters and output variables by a polynomial basis, which is specified by sampling the system and does not need any insight into the mathematical description of the system itself (in fact, a mathematical description is not even necessary, one can also describe empirical systems in the real world). This method has been implemented into the Python based software package pyGPC.
In the field of non-invasive brain stimulation, for example, we have published a comprehensive study that investigates the influence of uncertainties concerning the electric properties of brain tissues with respect to the electric fields induced in the brain (Saturnino et al. 2019). We show that TMS fields are generally less affected by conductivity variations than tDCS fields. For both TMS and tDCS, conductivity uncertainty causes much higher uncertainty in the magnitude as compared to the direction and overall spatial distribution of the electric field. Whereas the TMS fields were predominantly influenced by gray and white matter conductivity, the tDCS fields were additionally dependent on skull and scalp conductivities.

The figure shows some results of the uncertainty and sensitivity analysis for the TMS and TES field calculation. Column 1: Schematic stimulation configurations. Column 2: Mean value and relative standard deviation (RSD) of the electric field on the cortical surface taking into account the uncertainties of the conductivities taken from the literature. While for TMS a significant uncertainty only occurs at locations with low field strength (Sulci), TES field calculations in a larger area are to be assumed as uncertain. Columns 3-5: Relative contributions of different tissue types to the uncertainty. While TMS is influenced to a certain extent by the grey matter (GM) and white matter (WM), TES is strongly influenced by GM, compact bone (HB) and scalp (S) and moderately by WM and CSF. In all cases, spongy bone (SB) has little influence on the electric field.
Despite the widespread use of transcranial magnetic stimulation (TMS), the precise cortical locations underlying the resulting physiological and behavioral effects are still only coarsely known. Focusing on the motor cortex, we presented a novel method to reliably determine the effectively stimulated cortical site at the individual subject level (see here). We used extensive uncertainty and sensitivity analyses to verify the robustness of the method and identify the most critical model parameters. The uncertainty and sensitivity analyses confirmed robust hotspots on the gyral crowns, extending to upper parts of the sulcal wall of M1. The maxima of the means coincided well with the results of the deterministic case. The relative standard deviation (RSD) in the hotspots on the gyral crowns varied between 10-25%, depending on the subject. Decomposing the variance by origin revealed a strong contribution from GM and WM conductivity as well as from the measured I/O curves. This is in line with the previous study, which showed that the electrical conductivity of GM and WM are the most influential parameters considering the induced electric field in grey matter (Saturnino et al., 2019).
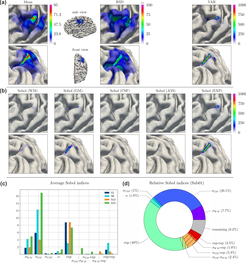
The figure shows results of the uncertainty and sensitivity analysis of the congruence factor determined for one subject of the study. (a) Expected value (Mean) of the congruence factor, relative standard deviation (RSD), and variance (VAR) of the congruence factor. (b) Spatial distributions of the absolute first order Sobol indices. The Sobol index maps resulting from uncertainties in the experimental data are summarized into one Sobol index map Sobol (EXP). (c) Average first order Sobol indices for subjects Sub01 (shown here), Sub08, Sub12 and Sub15. The average was computed over the elements in the ROI (d) Relative first order Sobol indices averaged over the ROI. For (a) and (b) two different perspectives are shown (top and bottoms rows), to improve visibility of the effects.

